April 2022 — In survey questionnaires, sampling design refers to the strategy or plan to identify to select a sample. Sampling designs fall into two camps, probability, and non-probability-based sampling designs. Probability-based sampling is defined by all potential respondents (i.e., elements) having an equal chance of selection to participate in the sample. The equal chance of selection results in the sample being representative and generalizable.
Non-probability-based sampling is defined as the opposite. Elements of the population are not guaranteed an equal chance of selection, and therefore the sample is not representative nor generalizable. The value of a non-probability-based sampling design is related to the ability to collect information from either knowledgeable or hard-to-reach populations.
Non-Probability Sampling
Researchers and practitioners can use several non-probability sampling approaches, including convenience sampling, purposive sampling, and snowball sampling.
How to do a convenience sample?
A convenience sample is what it sounds like. It is a group selected based on their availability and the ease to get them to participate. This approach is not a recommended method and should not be utilized if you want to generalize the findings to a population. The best use of this sampling design is to employ when pilot testing the survey instrument.
How to do a purposive sample?
A purposive sample is selecting participants based on an important characteristic. Researchers and practitioners utilize this approach when ascertaining information about a specific group that may be knowledgeable of the topic. For example, if you were studying downtown consumers, but wanted to understand this topic from the perspective of the business owners, you would need business owners to complete the survey. The population of downtown businesses will be much smaller than the population of shoppers, and therefore, you do not need to utilize a probability-based sampling strategy. As the population size increases or the sample size decreases, you will need to be careful about how you present your findings.
How to do a snowball sample?
A snowball sample conjures up the image of building layers, which is what this sampling strategy does. Researchers and practitioners use this sampling strategy if they do not have a known or clear sampling frame. If you wanted to survey what leadership in the community thinks about the downtown business district, you will need to contact leaders. There will be no established sampling frame of leaders and the population will not be clear. Community leaders could include elected and appointed officials, business and economic leaders, or social and civic leaders. Communities usually do not keep a list of leaders. The method is very straightforward. You purposively choose known leaders to participate, and upon completion, ask for a recommendation of other leaders. You keep doing this, i.e., adding layers to the snowball, until you have exhausted the list of leaders. This process will occur when you begin to receive the same names and rarely any new recommendations.
Probability Sampling
Similarly, there are many types of probability-based sampling designs. Researchers or practitioners utilize probability-based sampling designs when they want to say something about a larger population with relative confidence that the findings are generalizable to and representative of the population. Some of the more common and easier to develop and execute strategies are simple random sampling, systematic sampling, and stratified sampling.
How to do a simple random sample?
The easiest of these sampling strategies is a simple random sample where elements are selected at random. This approach works well if the population is relatively homogenous. There are several ways to choose potential participants from your population. For demonstration, let us assume you have a population of 10,000 households in the community and a sampling frame that captures all 10,000. You know you want roughly a +/-3.0% margin of error, so you aim for 1,000 total respondents (note, this assumes that everyone who receives the survey will complete it. This is not going to happen. Therefore a real survey project would require selecting more households to include in your sample).
You would take the list of 10,000 households, sequential number all of them from 1 to 10,000, and then use a random number generator to select your sample. Several online random number generators allow you to set the parameters (i.e., your number range and how many randomly produced numbers within this range you need). Excel also has several ways to select participants at random. For example, adding a column to your spreadsheet next to the field (in this case, household address), and then using a formula to produce a distinct and random number. In either case, with the random number generator or using a formula in Excel, you would use the random numbers to select your sample of 1,000.
How to do a systematic sample?
A systematic sample is also an easy sampling strategy. It is most useful with homogenous groups and where there is not a built-in issue with systemic bias in the sampling frame. Again, using the example of wanting to survey households in a community of 10,000, one would start this process by identifying their intended sample size. To meet your ideal margin of error, you decide on 1,000 households.
Now that you have the sampling frame and know your sample size, you need to identify your sampling interval, or the number used to select households from your sampling frame. The sampling interval is calculated by dividing the population size by the intended sample size.
10,000 / 1,000 = 10
You would then need to randomly generate a number within the sampling interval (i.e., 1-10). For demonstration purposes, let us assume your random start number is 7. You would select the 7th household from your list and then select every 10th household from the sampling frame as part of your sample (e.g., 17th, 27th, 27th, and so on). As stated earlier, this works with homogeneous populations. It will not work if your sampling frame has a built-in systemic problem. For example, if every 10th household falls on a corner lot with a larger yard and possibly a higher home value, you may run into a systemic sampling error that could bias your results.
How to do a stratified sample?
A stratified sampling design is appropriate when the population is heterogeneous and where the researcher can identify different segments. Stratified sampling can be paired with either simple random or systematic sampling. For demonstration, let us assume you know there are two types of households in your community that tend to have very different experiences and shopping behaviors. This difference is between homeowners and renters. In your sampling frame, you can identify which households are homeowners and which ones are renters. You would separate these two groups into two separate lists. Let’s say 5,000 households own and 5,000 rent. You would then assign every household in each group a number – e.g., homeowners numbered 1-5,000, and renters numbered 1-5,000.
At this point, you can either utilize a simple random sample or a systematic sample by following the steps above. You know you are targeting 1,000 total participants, and because the sampling frame is divided into two equal-sized sub-groups, you will need to select 500 participants from each group.
In the case of a simple random sample, you would generate two different lists of 500 randomly selected numbers. As for the systematic sampling strategy, you would find the sampling interval by dividing the subgroup by the subgroup sample size (i.e., 5,000 / 500 = 10). You would then generate a random number for each subgroup between 1-10 to start the sample, counting every 10th household until you have 500 owners and 500 renters.
Weighting Your Data
Despite your best efforts, you will undoubtedly run into challenges with sampling all meaningful segments of your population. Sometimes this is because you did not anticipate a subgroup in the population. Or, you did not know a group would participate at a lesser rate than another. There are ways to correct some of these errors by weighting your data after you have collected it. The key to this process is to have a parameter for the population. A parameter is a measure of the population; whereas, a statistic is a measure of the sample. The easiest way to ascertain a population parameter is to utilize US Census estimates. Parameters commonly used to weight survey data include income, education, gender, and race. There are, of course, other population estimates you could utilize (for an overview of weighting methods see the Pew Research Center).
Continuing with the example of sampling households, let us assume you did not know or anticipate a meaningful difference between homeowners and renters. Specifically, you did not realize that there would be what appears to be a difference between older homeowners, younger homeowners, older renters, and younger renters. Furthermore, you can see in the data that younger respondents are not filling out the questionnaire regardless of renting or owning at the same rate as older respondents. If you know the population parameter for owning and renting and age, you can weight your data to adjust your dataset to reflect the population. Here is a hypothetical example:
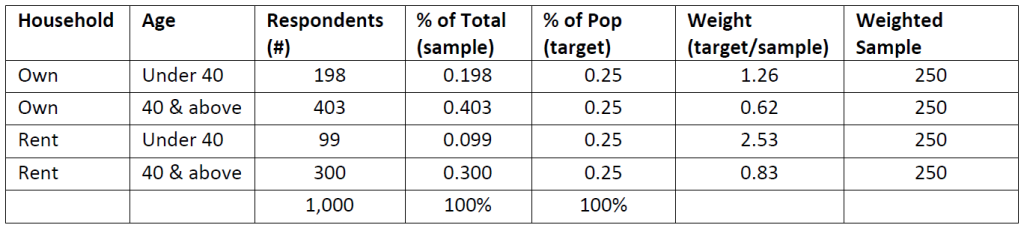
Respondents column – number of respondents per category (e.g., 198 of the 1,000 total respondents own their home and are under 40 years old).
% of Total – the number of respondents within a category divided by the total sample (e.g., 198 / 1,000 = .198, or 19.8%).
% of Pop – the percentage of the population that comes from population parameters such as ones obtained through the US Census.
Weight – the weighted number to adjust for sampling error (i.e., target divided by sample, or .25 / .198 = 1.26). This number would be applied to responses based on the identified characteristics of the household and age.
Weighted Sample – this is the number that reflects what the sample distribution would be if it matched the population percentages (e.g., 198 * 1.26 = 250).
Depending on the program you are using to store and analyze your data, there are different ways to apply these weights to your data analysis. If you do not have the experience or confidence to work through this process, we advise you to reach out to someone with this expertise.
About the Toolbox and this Section
The 2022 update of the toolbox marks over two decades of change in our small city downtowns. It is designed to be a resource to help communities work with their Extension educator, consultant, or on their own to collect data, evaluate opportunities, and develop strategies to become a stronger economic and social center. It is a teaching tool to help build local capacity to make more informed decisions.
This free online resource has been developed and updated by over 100 university educators and graduate students from the University of Wisconsin – Madison, Division of Extension, the University of Minnesota Extension, the Ohio State University Extension, and Michigan State University – Extension. Other downtown and community development professionals have also contributed to its content.
The toolbox is aligned with the principles of the National Main Street Center. The Wisconsin Main Street Program was a key partner in the development of the initial release of the toolbox. One of the purposes of the toolbox has been to expand the examination of downtowns by involving university educators and researchers from a broad variety of perspectives.
The current contributors to each section are identified by name and email at the beginning of each section. For more information or to discuss a particular topic, contact us.












 Focus Group Analysis Tips
Focus Group Analysis Tips Developing Questions for Focus Group Interviews
Developing Questions for Focus Group Interviews A Community Education Approach
A Community Education Approach Business Recruitment
Business Recruitment